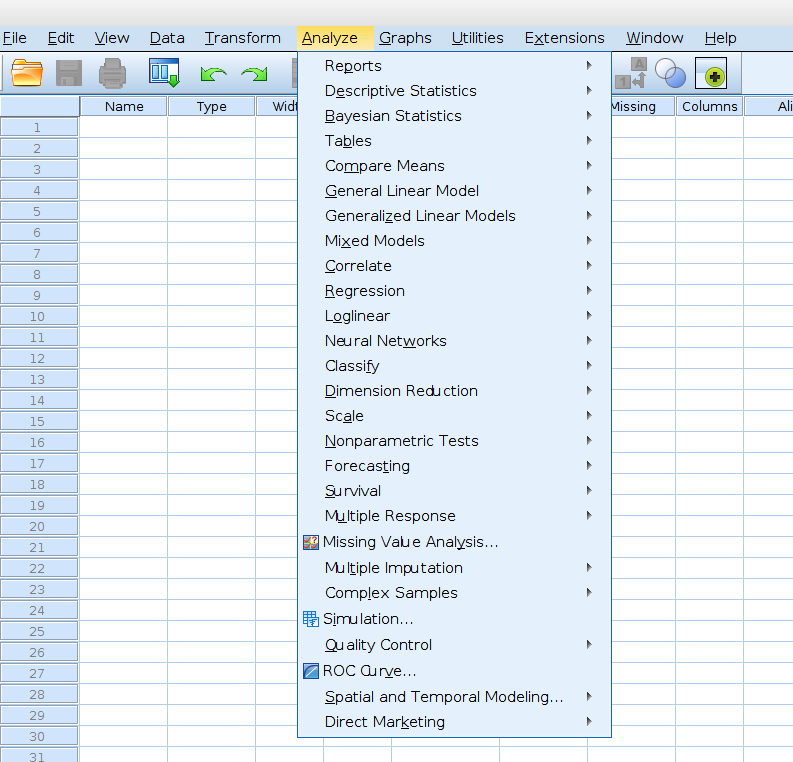
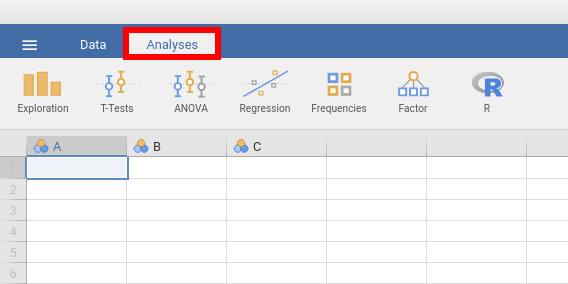
Comparison of analyses available in SPSS and jamovi

SPSS (version 27) The overview covers functions from SPSS Base (99$) and Advanced (79 US$), i.e. 178 US$ / user and month.	jamovi (versjon 2.0)
	Already at first glance, it becomes clear that jamovi currently has fewer features than SPSS. But: (1) There is a (ever increasing) made available via modules (press the “+” sign in the right upper corner of the jamovi window to add them) and (2) The features implemented already cover “standard” needs (90% of the most common analyses used in psychology). Feel free to check out which modules are available: There is also quite a wealth of modules covering functions that are not available in SPSS but very useful (e.g., for meta-analyses; MAJOR). If you are willing to use some R code (e.g., in conjunction with the jamovi-module Rj) then you can (most presumably) do every analysis you could imagine.
Reports
Reports → Codebook	N/A
Reports → OLAP Cubes	N/A
Reports → Case summaries	Exploration → Descriptives has the same functionality
Reports → Reports Summaries in Rows	N/A
Reports → Reports Summaries in Columns	N/A
Descriptive Statistics
Descriptive Statistics → Frequencies	Exploration → Descriptives combines all three procedures tick «Frequency tables» to get an output that is similar to that of «Frequencies» in SPSS
Descriptive Statistics → Descriptives
Descriptive Statistics → Explore
Descriptive Statistics → Crosstabs	Frequencies → (Contingency tables) → Independent samples
Descriptive Statistics → Ratio	N/A
Bayesian Statistics
	requires the jamovi-module «jsq»
Bayesian Statistics → One Sample Normal	T-Test → Bayesian One Sample T-Test
Bayesian Statistics → One Sample Binomial	Frequencies → Bayesian Proportion Test
Bayesian Statistics → One Sample Poisson	Frequencies → Bayesian Contingency Tables
Bayesian Statistics → Related Sample Normal	T-Test → Bayesian Paired Samples T-Test
Bayesian Statistics → Independent Samples Normal	T-Test → Bayesian Independent Samples T-Test
Bayesian Statistics → Pearson Correlation	Regression → Bayesian Correlation Matrix / Bayesian Correlation Pairs
Bayesian Statistics → Linear Regression	Regression → Bayesian Linear Regression
Bayesian Statistics → One-way ANOVA	ANOVA → Bayesian ANOVA (can handle several factors while SPSS is limited to one factor)
Bayesian Statistics → Log-Linear Models	Frequencies → Bayesian Log-Linear Regression
Compare Means
Compare Means → Means…	Exploration → Descriptives replaces / integrates that functionality, choose the drop-down menu «Statistics» and set ticks at «Mean», «N» and «Std. deviation»
Compare Means → Independent-Samples T Test	T-Test → Independent Samples T-Test
Compare Means → Paired-Samples T Test	T-Test → Paired Samples T-Test
Compare Means → One-Sample T Test	T-Test → One Sample T-Test
Compare Means → One-Way ANOVA	ANOVA → One-Way ANOVA
General Linear Model
General Linear Model → Univariate	ANOVA → One-Way ANOVA
General Linear Model → Multivariate	ANOVA → MANCOVA
General Linear Model → Repeated Measures	ANOVA → Repeated Measures ANOVA
General Linear Model → Variance Components	N/A
Generalized Linear Models
	requires the jamovi-module «GAMLj» (General Analyses for the Linear Model in jamovi)
Generalized Linear Models → Generalized Linear Models
Generalized Linear Models → Generalized Estimating Equations
Mixed Models
	requires the jamovi-module «GAMLj» (General Analyses for the Linear Model in jamovi)
Mixed Models → Linear
Mixed Models → Generalized Linear
Correlate
Correlate → Bivariate	Regression → Correlation Matrix
Correlate → Partial	Regression → Partial Correlation
Correlate → Distances	N/A
Regression
Regression → Automatic Linear Models	N/A
Regression → Linear	Regression → Linear Regression
Regression → Ordinal	Regression → (Logistic Regression) → Ordinal Outcomes
Regression → Curve Estimation
Regression → Partial Least Squares
Loglinear
Loglinear → General	Frequencies → Log-Linear Regression
Loglinear → Logit
Loglinear → Model Selection
Classify
Classify → Nearest Neighbor	N/A
Classify → Discriminant	N/A, can be calculated using R-code and the R-library «MASS»
Classify → TwoStep Cluster	N/A
Classify → Hierarchical Cluster	N/A, can be calculated using R-code and the R-library «pvclust»
Classify → K-Means Cluster
Dimension Reduction
Dimension Reduction → Factor	Factor → (Data reduction) → Principal Component Analysis Factor → (Data reduction) → Exploratory Factor Analysis 1
Scale
Scale → Reliability Analysis	Factor → (Scale analysis) → Reliability analysis
Scale → Multidimensional Scaling	N/A
Nonparametric Tests
Nonparametric Tests → One Sample	N/A, the tests itself are available (see below), but not a common start menu that allows a selection based on your data (e.g., between- or within-subject)
Nonparametric Tests → Independent Samples
Nonparametric Tests → Related Samples
Nonparametric Tests → Legacy Dialogs → Chi-Square	Frequencies → (One Sample Proportion Tests) → N Outcomes (x² goodness of fit)
Nonparametric Tests → Legacy Dialogs → Binomial	Frequencies → (One Sample Proportion Tests) → 2 Outcomes (Binomial test)
Nonparametric Tests → Legacy Dialogs → Runs	N/A
Nonparametric Tests → Legacy Dialogs → 1-Sample K-S	N/A, Shapiro-Wilks available under Exploration → Descriptives, choose drop-down menu «Statistics» and tick «Shapiro-Wilks»
Nonparametric Tests → Legacy Dialogs → 2 Independent Samples	T-Test → Independent Samples T-Test, set tick-box «Mann-Whitney U»
Nonparametric Tests → Legacy Dialogs → 2 Related Samples	T-Test → Paired Samples T-Test, set tick-box «Wilcoxon Rank»
Nonparametric Tests → Legacy Dialogs → K Independent Samples	ANOVA → (Non-Parametric) → One-Way ANOVA (Kruskal-Wallis)
Nonparametric Tests → Legacy Dialogs → K Related Samples	ANOVA → (Non-Parametric) → Repeated Measures ANOVA (Friedman)
Survival
	requires the jamovi-module «Death watch»
Survival → Life Tables
Survival → Kaplan-Meier
Survival → Cox Regression
Survival → Cox w/ Time-Dep Cov
Multiple Response
Multiple Response → Define Variable Sets	N/A
Multiple Response → Frequencies
Multiple Response → Crosstabs
ROC Curve
ROC Curve	N/A, accessible via R packages (e.g., ROCR eller pROC)
Simulation
Simulation	N/A
Spatial and Temporal Modeling
Spatial and Temporal Modeling → Spatial Modeling	N/A

1

Whereas SPSS puts both methods into one procedure (FACTOR) makes jamovi a conceptual difference between Principal Component Analysis aiming at data reduction (i.e., reducing the number of dimension that are required to describe the data) and Exploratory Factor Analysis aiming at extracting underlying latent variables.